Год сдачи: 2009 Информация о файлах в архиве: программа,блок-схема с приложением Математическая постановка.
Метод левых прямоугольников.
Необходимо найти значение определенного интеграла с помощью метода левых прямоугольников. По условию, a= -π/2, b= π/2, n=5. Разделим отрезок [-π/2, π/2] на 5 равных частей, т.е. на 5 элементарных отрезков. Длина каждого элементарного отрезка h=(b-a)/n= (π/2-(-π/2))/5=0.63. Получаем следующие точки деления: х0=-1.57, x1=-0.94,x2=-0.31,x3=0.31,x4=0.94,x5=1.57. Эти точки будем называть узлами. Вычислим значение функции f(x) = 1/(1+cos(x)) в этих узлах , обозначим их y0,y1,…,yn:
y0((-1.57)=1; y1(-0.94)=0.63; y2(-0.31)=0.51; y3(0.31)=0.51; y4(0.94)=0.63; y5(1.57)=1.
Числа y0,y1,…,yn являются ординатами точек графика функции, соответствующие абсциссам x0,x1,x2,xn. Площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n=5 прямоугольников.
Таким образом, вычисление определенного интеграла сводится к нахождению суммы n=5 элементарных прямоугольников.
Формула левых прямоугольников:
S≈≈ y0*h+ y1*h+ y2*h+...+yn-1*h≈ h* (y0+ y1+ y2+...+ yn-1)
S≈≈0.63*(1+0.63+0.51+0.51+0.63)≈2,07. Заключение.
Таким образом, использование численных или приближенных методов решения определенного интеграла как компьютерных алгоритмов, владение навыками программирования, например, в среде Turbo Pascal, дает возможность разработки компьютерных программ и приложений для решения определенного интеграла. Усиленные мощью современные компьютеры позволяют получить этот результат за считанные секунды. Содержание
1. Математическая постановка. 3
2. Блок- схема алгоритма. 4
3. Листинг программы. 8
4. Контрольный пример. 13
5. Руководство пользователя. 14
6. Заключение. 18
7. Список литературы. Программа на Pascal'e Расчитывающая интеграл методом левых прямоугольников 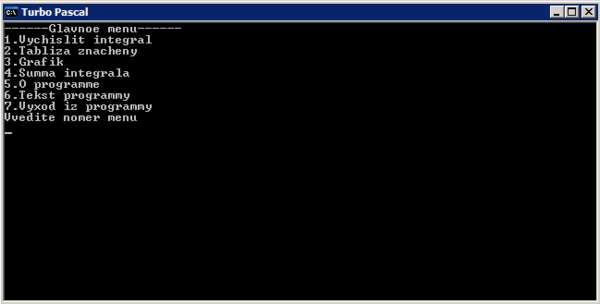
|
